Masters and delta sets - a note to self
Here’s another thing which I always forget when I’m building variable fonts, and when I say “building variable fonts”, I mean “building things which build variable fonts”.
We all know that each glyph in variable font is made up of the contour of the default master, stored in the glyf table, and then, for each master, the deltas between each point on the default contour and the contour for that master, stored in the gvar table, right?
WRONG. Horribly wrong.
Do not do this.
Or rather: deceptively correct in simple cases, which is why I always forget it, but horribly wrong in the general case. Specifically, if you put your masters in at the ends of your axes like this, it’ll work:
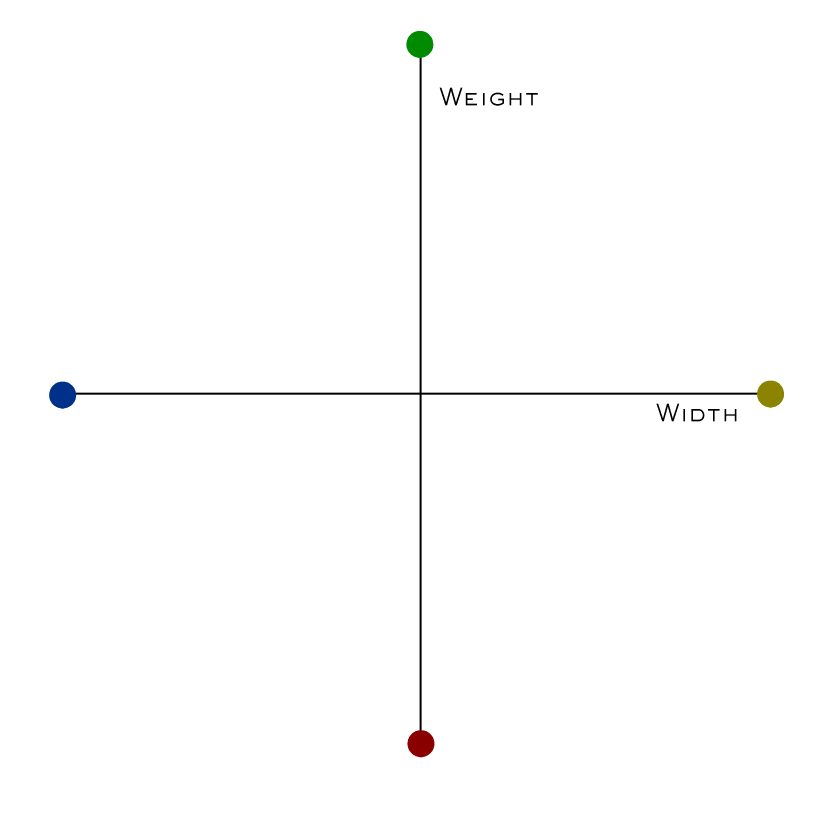
But the moment you start putting masters into the corners (or worse, the middle), like this:

then it all falls apart…

No, it’s really not meant to look like that.
(The really annoying thing is that I solved this problem once already when I wrote Babelfont, and then last week when I came to implementing a new variable font builder in Rust, I completely forgot why the problem was happening and how to solve it. So, once again, I’m writing this down to try to ensure that I don’t confuse myself again next time I come up against this.)
Why is this happening? The simple answer is that the deltas stored inside a font are not deltas between the default master and other design masters. But to find out what they are, let’s take a look using the example of Nunito again. Here is its master configuration in designspace coordinates:
| Master | Weight | Italic |
|---|---|---|
| ExtraLight.ufo | 42 | 0 |
| M500.ufo | 125 | 0 |
| M1000.ufo | 208 | 0 |
| ExtraLightItalic.ufo | 42 | 9 |
| M500SlantItalic.ufo | 125 | 9 |
| M1000SlantItalic.ufo | 208 | 9 |
One default master (the ExtraLight), and five variation masters. Notably, there are intermediate masters, wght=125,ital=0 and wght=125,ital=9. Let’s just think about the weight axis and ignore the italic for now.
The key to understanding variable font interpolation is to ask the question “How much should each master contribute at a given point?”
So at wght=42, none of the variation masters should contribute any deltas. At the other end of the axis, wght=208, the M1000.ufo master should contribute all of its deltas, and the M500.ufo master should contribute none. Those cases are obvious. When we’re sitting on an intermediate master, wght=125, that master (M500.ufo) master should contribute all of its deltas, and nothing else on the weight axis should contribute any deltas.
Now think about the midpoints between masters. At wght=83.5, the M500.ufo master should contribute half of its deltas and the M1000.ufo master should still not be involved in interpolation at all, and hence not contribute any deltas. Still quite obvious.
At the other midpoint, wght=166.5, things start to get non-obvious. You might think that things are set up so that M500.ufo contributes all of its deltas, and then M1000.ufo contributes half of its deltas, but they wouldn’t be half of the deltas between M1000 and the default master any more, but half of the deltas between itself and M500.ufo, and that gets really awkward with multiple axes. Instead, the M500.ufo master should contribute half of its deltas and the M1000.ufo master should also contribute half its deltas. And as we established above, when we’re at the far end of the axis, we want the M500.ufo master to contribute nothing. So Semibold is not “go to Regular and then go half way from there to Bold”, but a blend of half of Regular and half of Bold. (Convince yourself that this is the case before going further.)
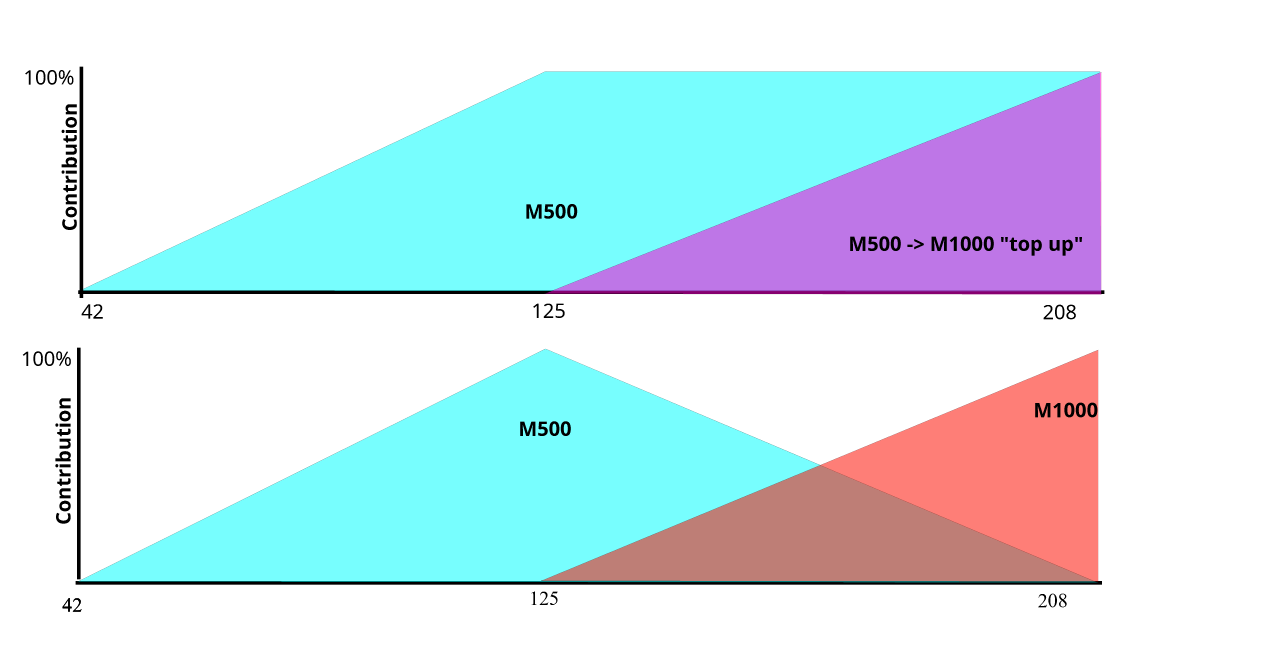
We don’t do the top picture. We do the bottom picture.
So these masters provide contributions in triangular patterns, with the output being the sum of the contributions of all masters. These triangles - sometimes called “regions” or “tents” - have a start point, a peak point (100% contribution) and an end point. These start/peak/end tuples are also called supports, because in mathematics a support is the region for which a function is active.
Obviously, a master at location X has 100% contribution at X. But the starts and end points is less obvious. Note that the M1000 master does not start contributing until after we’ve got past the intermediate master. The mistake I’ve made, both times I’ve tried implementing this, is to treat each master independently, throw in all the deltas, and hope for the best. Laurence Penny’s wonderful Samsa tool helpfully shows the tents for us, and you can see clearly what I did wrong:
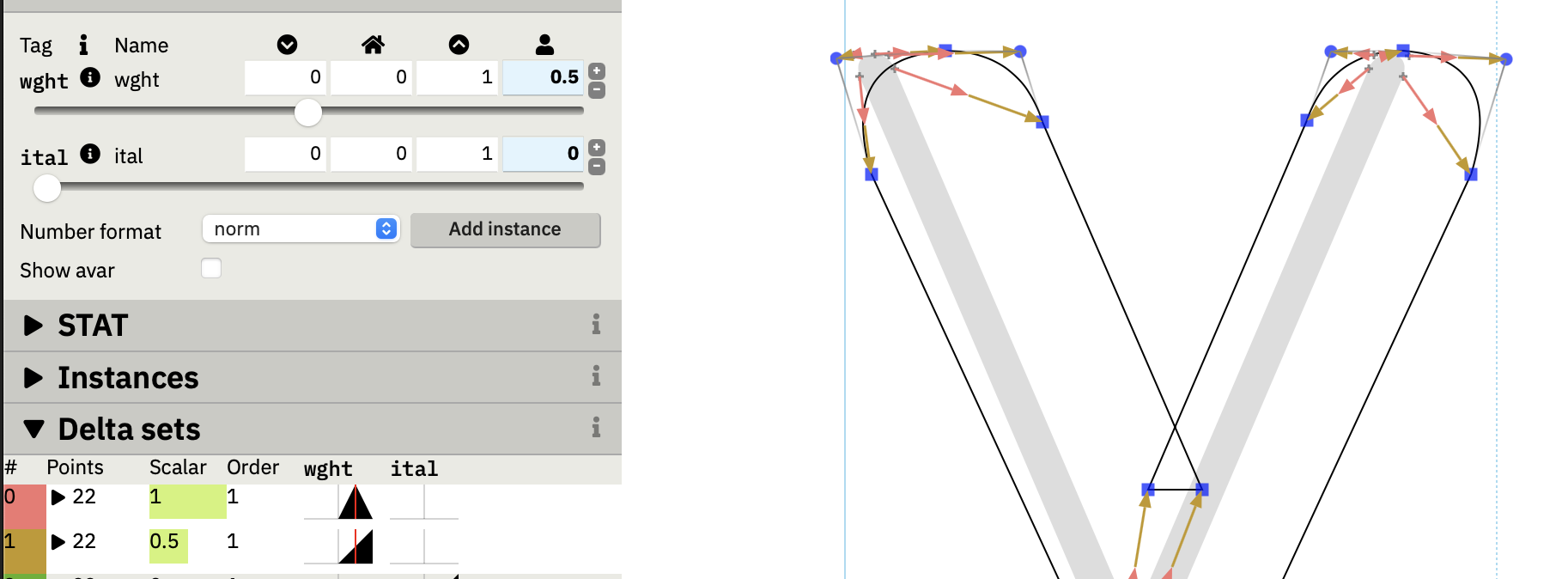
The brown arrows should not be there.
You can see that at halfway down the weight axis, I have 100% contribution from M500.ufo, which is great, but I also have 50% contribution of M1000.ufo, which is not so great. You can see why I made the mistake: if the intermediate master wasn’t there, I would want 50% of the M1000.ufo master to get me halfway down the weight axis. But with the intermediate master, I’m already where I want to be, so the contribution should have been zero, but instead I’ve ended up by applying two sets of deltas instead of one.
So setting the starts and ends of the tents requires looking at all the masters together and determining the values for each master depends on its position in the designspace and its relationship to all the other masters.
Now let’s think about the italic axis, and this is where it gets really horrible because we now have masters which contribute to two axes at once. Our final two masters:
| Master | Weight | Italic |
|---|---|---|
| M500SlantItalic.ufo | 125 | 9 |
| M1000SlantItalic.ufo | 208 | 9 |
tell us what should happen as both weight and slope varies.
In this case, we need to not only set the tents correctly, but we also need to change the deltas themselves.
Let’s suppose we’re at wght=208, italic=9. What contributions should we expect? Here’s one option: M1000SlantItalic.ufo contributes 100% and gets us to the place we want to be, and nothing else contributes anything. Unfortunately it turns out to be impossible to get that to work and to create linear, triangular, tents for all the other masters to work properly. I can’t explain why not, because honestly, it’s starting to get beyond me at this point.
Instead, here’s what actually happens in OpenType: M1000.ufo contributes 100% (to get us to the end of the weight axis), and ExtraLightItalic.ufo contributes 100% (to get us to the end of the italic axis), and then M1000SlantItalic.ufo also contributes 100% of its deltas, but - and this is the critical bit - the deltas here aren’t the deltas between the default master and the M1000SlantItalic.ufo (otherwise we would have a double application again). The deltas we write for the deltaset representing the M1000SlantItalic.ufo master are actually a kind of correction value - they’re the deltas between where we already got to when we applied 100% of M100.ufo plus 100% of ExtraLightItalic.ufo, and where we want to get to based on the points in M1000SlantItalic.ufo.
Samsa calls these deltasets “order 2 deltasets”, because they’re deltasets based on another delta set. This is where the concept of higher order interpolation comes from, which you might have heard about elsewhere.
The other mistake I make when implementing variable font builders is to just throw in all the deltas from default master to M1000SlantItalic.ufo, instead of doing this higher-order delta operation. This results in massive deltas, which also get doubly applied because now there’s no sensible way to compute the start/end regions, and the end result is a complete mess:
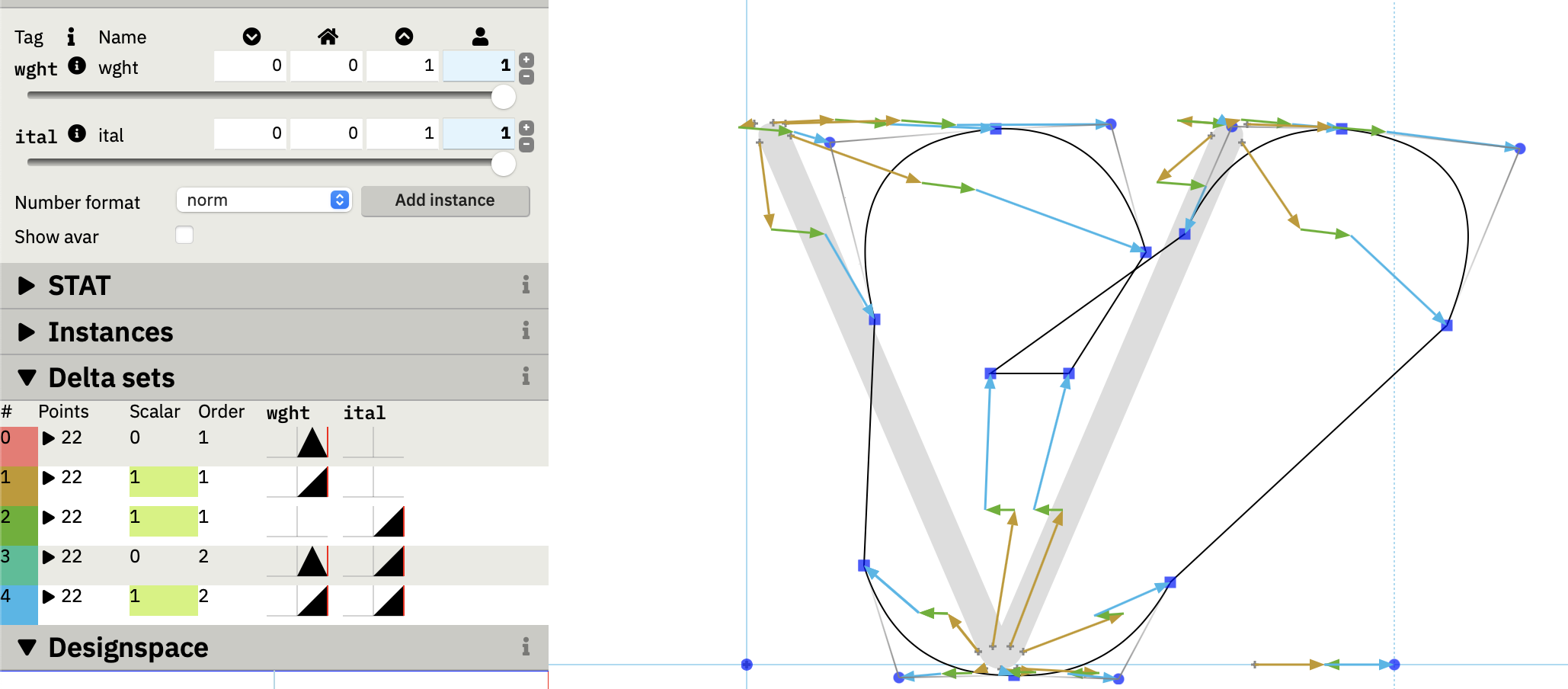
The way to fix both mistakes is to use a proper variation model, which computes both the supports and the correct deltas by considering all the masters in combination and by applying higher-order deltas. Which is why I spent two days this week porting fontTools.varLib.models, first to TypeScript and then to Rust.
Maybe next time, I’ll actually remember these problems, and build in the variation model from the start.